 |
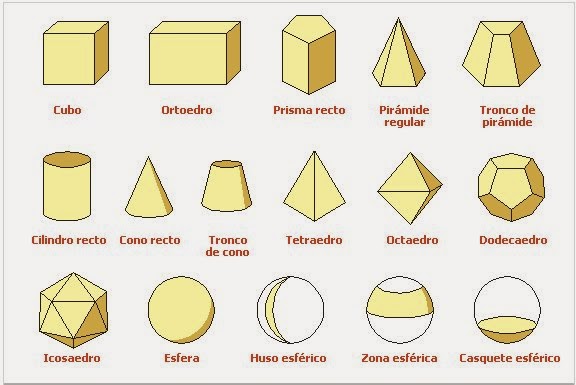
| Cuerpos Geométricos |
Los cuerpos geométricos se pueden clasificar a su vez en poliedros y cuerpos geométricos redondos o no poliedros.
Poliedros
Los poliedros o cuerpos planos, son cuerpos geométricos cuyas caras son todas figuras geométricas exclusivamente planas. Entre los más conocidos se encuentran los siguientes:
Sólidos platónicos
.jpg) |
| Tabla - Sólidos Platónicos |
Los sólidos platónicos o regulares son poliedros convexos tal que todas sus caras son polígonos regulares iguales entre sí, y en que todos los ángulos sólidos son iguales. Reciben este nombre en honor al filósofo griego Platón (ca. 427 a. C./428 a. C.-347 a. C.), a quien se atribuye haberlos estudiado en primera instancia. También se conocen como cuerpos platónicos, cuerpos cósmicos, sólidos pitagóricos, sólidos perfectos, poliedros de Platón o, en base a propiedades geométricas, poliedros regulares convexos.
Los sólidos platónicos son el tetraedro, el cubo (o hexaedro regular), el octaedro (o bipirámide cuadrada si se incluyera en la nomenclatura de sólidos de Johnson), el dodecaedro y el icosaedro (o bipirámide pentagonal giroelongada si se incluyera en la nomenclatura de sólidos de Johnson). Esta lista es exhaustiva, ya que es imposible construir otro sólido diferente de los cinco anteriores que cumpla todas las propiedades exigidas, es decir, convexidad y regularidad.
Pirámide
 |
| Tipos de Pirámide y Desarrollo |
Una pirámide es un poliedro limitado por una base, que es un polígono con una cara; y por caras, que son triángulos coincidentes en un punto denominado ápice.
El ápice o cúspide también es llamado vértice de la pirámide, aunque una pirámide tiene más vértices, tantos como el número de polígonos que lo limitan.
El ápice o cúspide también es llamado vértice de la pirámide, aunque una pirámide tiene más vértices, tantos como el número de polígonos que lo limitan.
- Una pirámide recta es un tipo de pirámide cuyas caras laterales son triángulos isósceles. En este tipo de pirámides la recta perpendicular a la base que pasa por el ápice corta a la base por su circuncentro.
- Una pirámide oblicua es aquella en la que no todas sus caras laterales son triángulos isósceles.
- Una pirámide regular es una pirámide recta cuya base es un polígono regular.
- Una pirámide convexa tiene como base un polígono convexo.
- Una pirámide cóncava tiene como base un polígono cóncavo.
- Existen tres tipos de pirámides cuyas caras son triángulos equiláteros, con bases de 3, 4 y 5 lados respectivamente. Un tetraedro regular es una pirámide cuyas caras (base y caras laterales) son triángulos equiláteros.
| Prismas |
En geometría, un prisma es un poliedro con una base poligonal de n lados, una copia de traslación (no en el mismo plano que la primera), y otras n caras (todas necesariamente deben ser paralelogramos) que une los lados correspondientes de las dos bases. Todas las secciones transversales paralelas a las caras de la base son iguales. Los prismas se nombran para su base, por lo que un prisma de base pentagonal se llama un prisma pentagonal. Los prismas son una subclase de los prismatoides.
Redondos
Los cuerpos redondos son aquellos que tienen, al menos, una de sus caras o superficies de forma curva. Entre los más conocidos se encuentran:
Esfera
 |
| La Esfera |
La esfera, como superficie de revolución, se genera haciendo girar una superficie semicircular alrededor de su diámetro (Euclides, L. XI, def. 14).
Esfera proviene del término griego σφαῖρα, sphaîra, que significa pelota (para jugar). Coloquialmente hablando, se emplea la palabra bola, para describir al cuerpo delimitado por una esfera.
Cilindro
 |
| Cilindro |
En geometría, un cilindro es una superficie de las denominadas cuádricas formada por el desplazamiento paralelo de una recta llamada generatriz a lo largo de una curva plana, que puede ser cerrada o abierta, denominada directriz del cilindro.
Si la directriz es un círculo y la generatriz es perpendicular a él, entonces la superficie obtenida, llamada cilindro circular recto, será de revolución y tendrá por lo tanto todos sus puntos situados a una distancia fija de una línea recta, el eje del cilindro. El sólido encerrado por esta superficie y por dos planos perpendiculares al eje también es llamado cilindro. Este sólido es utilizado como una superficie Gausiana.
En geometría diferencial, un cilindro se define de forma general como cualquier superficie reglada generada por una familia uniparamétrica de líneas paralelas.
Si la directriz es un círculo y la generatriz es perpendicular a él, entonces la superficie obtenida, llamada cilindro circular recto, será de revolución y tendrá por lo tanto todos sus puntos situados a una distancia fija de una línea recta, el eje del cilindro. El sólido encerrado por esta superficie y por dos planos perpendiculares al eje también es llamado cilindro. Este sólido es utilizado como una superficie Gausiana.
En geometría diferencial, un cilindro se define de forma general como cualquier superficie reglada generada por una familia uniparamétrica de líneas paralelas.
Toro
 |
| Torus - Toro |
En geometría, un toro o torus es una superficie de revolución generada por una circunferencia que gira alrededor de una recta exterior coplanaria (en su plano y que no la corta). La palabra «toro» proviene del vocablo en latín torus, el cual en castellano significa «bocel» o «murecillo», que es una moldura redondeada de la basa, con forma de hogaza de pan. Muchos objetos cotidianos tienen forma de toro: un dónut, una rosquilla, la cámara de un neumático, etc.
Cono
 |
| Cono |
En geometría, un cono recto es un sólido de revolución generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos. Al círculo conformado por el otro cateto se denomina base y al punto donde confluyen las generatrices se llama vértice o cúspide. Otra definición ( mas simple ) : Cuerpo geometrico
Superficie cónica se denomina a toda superficie reglada conformada por el conjunto de rectas que teniendo un punto común (el vértice), intersecan a una circunferencia no coplanaria.
Superficie cónica se denomina a toda superficie reglada conformada por el conjunto de rectas que teniendo un punto común (el vértice), intersecan a una circunferencia no coplanaria.
________________________________________________
Recursos - Videos
Los Prismas
Paralelogramo
Área Polígono Regular
Área del Triángulo
El Prisma
Calculando el volumen de un sólido de revolución
Volumen y área de prismas y pirámides
________________________________________________
Actividades Interactivas
 |
| Clic en la imagen |
 |
| Clic en la imagen |
Los Cuerpos Geométricos
El Cilindro, el cono y la esfera
El Volumen
El Volumen - Wikisaber
Plano de simetría
Cuerpos Geométricos
Área de prismas regulares.
Área de pirámides y de troncos de pirámide.
Área de cilindros.
Área de conos y troncos de cono.
Área de superficie esférica.
Volumen de los cuerpos. Unidades de volumen.
Volumen y capacidad.
Volumen de prismas.
Volumen de pirámides.
Volumen de cilindros y de conos.
Volumen de la esfera.
Practica ejercicios de áreas de figuras planas
________________________________________________
TEST y Tutoriales onLine
Test Geometría Sólidos
Cuerpos Geométricos y Volumen
Thtaquiz - Test
Teoría de Áreas y Volúmenes - Tutorial y Ejercicios
1. Tetraedro
2. Octoedro e icosaedro
3. Dodecaedro
4. Cubo y ortoedro
5. Prisma y pirámide
6. Tronco de pirámide
7. Cilindro, cono y tronco de cono
8. Esfera, huso y cuña
9. Casquete, zona y segmento esférico
_______________________________________________
PDFs
Desarrollo de cinco poliedros regulares
Desarrollo de un prisma y un antiprisma
Desarrollo del cuboctaedro y del icosidodecaedro
Desarrollo de los cinco poliedros regulares truncados
_____________________________
Fuentes: ASXKids ASXLab
EducarChile - Wikipedia